Predicting the future of excitation energy transfer in light-harvesting complex with artificial intelligence-based quantum dynamics

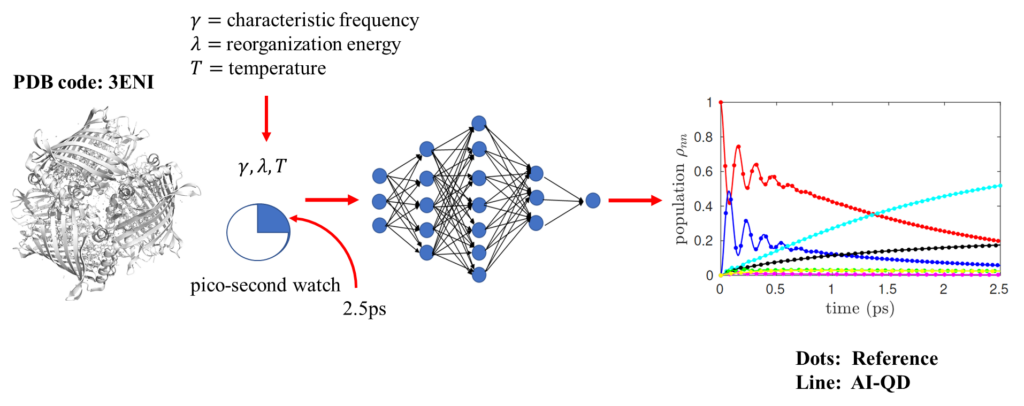
In the work published in Nature Communications, we have developed a blazingly fast artificial intelligence (AI)-based quantum dynamics (QD) approach with applications to excitation energy transfer in the well-known Fenna–Matthews–Olson (FMO) complex found in green sulfur bacteria.

All living organisms directly or indirectly depend on solar energy. Plants, algae and photosynthetic bacteria are blessed with highly efficient photosynthetic systems, transforming light energy into chemical energy. In general, a photosynthetic system consists of an antenna that captures sunlight, a reaction center and an exciton transfer complex that transfers light energy from the antenna to the reaction center in a highly efficient way. For some exciton transfer complexes such as Fenna–Matthews–Olsen (FMO) complex found in green sulfur bacteria, the transfer efficiency is reported to be near unity, attracted a lot of attention from the research community because of its possible applications in the so called biomimetic light-harvesting engineering focused on designing highly efficient organic solar devices. FMO complex is a trimer where each subunit consists of seven bacteriochlorophyll (BChl) molecules attached to their protein environments. Recently, an eighth BChl molecule is also reported but it has been shown that it does not play any significant role in the exciton energy transfer. In FMO complex, BChl molecules-1 and -6 are close to the antenna with an equal probability of getting initially excited while l molecules-3 and -4 are close to the reaction center.

Many quantum dynamics methods (to name a few, HEOM, SEOM, QuAPI and LTLME) have been developed to study excitation energy transfer in exciton transfer systems in particular FMO complex as its simplicity makes it a testbed for all of these approaches. In all traditional methods, one thing is common, all of them propagate dynamics iteratively (recursively), where the next time-step depends on the previous values and does not allow to predict the state of the system at some arbitrary time without propagating the trajectory, thus the recursive nature of these methods makes them computationally expensive. The recently proposed machine learning (ML)-based studies (Rodriguez and Kananenka 2021, Lin et al. 2021, and one of our own studies, Ullah and Dral 2021) are also iterative, thus prone to accumulation of error and, in addition, they need short-time trajectory (generated with traditional methods) as an input, thus even after having an ML-based approach, we still need traditional approaches.

In our study, we have proposed an artificial intelligence/machine learning (AI/ML)-based quantum dynamics (QD) method, which does not need any short-time trajectory as an input. Just by providing parameters such as a reorganization energy 𝜆, characteristic frequency 𝛾, temperature T etc., our AI-QD approach can predict the corresponding trajectory up to its asymptotic limit. Our proposed approach is non-iterative, which means that all time-steps are independent from each other, hence allows us to perform calculations in parallel, as a result enormously speeding up the calculations.  AI-QD approach not only can interpolate (predict excitation energy transfer for parameters, unseen to our trained model but lying within the range of parameters used in training) but also can extrapolate (predict excitation energy transfer for parameters outside the range of parameters used in training) to a good extent.

Our approach provides a new way to propagate quantum dynamics circumventing the need of iterative dynamics. Though it is true that we need to generate a lot of trajectories to train our model, however, by using farthest-point sampling, we can do better sampling of our parameter space, consequently leading to a small number of training trajectories sufficiently and uniformly covering the whole parameter space. In our case, we have used only 30% of our possible trajectories as a training set, enough to accurately predict excitation energy transfer for the remaining 70% of our parameter space (which we have taken as a test).

Importantly we have demonstrated the capability of AI-QD to efficiently screen a huge number (in our study half a million) of possible combinations resulting from interpolation and extrapolation to finding which parameters are better for efficient excitation energy transfer.

• Arif Ullah, Pavlo O. Dral, Predicting the future of excitation energy transfer in light-harvesting complex with artificial intelligence-based quantum dynamics, Nat. Commun. 2022, 13, 1930. DOI: 10.1038/s41467-022-29621-w.