Next Step: TB-SEMO Methods?

Johannes Margraf and I have published our perspective on what semiempirical molecular orbital (SEMO) methods are and should be approximating in the article[1] dedicated to the 70^th birthday of our PhD supervisor Tim Clark.

This topic is very close to Tim’s heart as he has significantly contributed to the field of SEMO method development and application. His unwavering enthusiasm and belief in the bright future of SEMO methods is contagious. Tim has also introduced us to the field, when we were his students. For this, I am very thankful to him and I wish Tim many more contributions to the field!

Back to our perspective. We first discuss how SEMO methods treat dynamic electron correlation in implicit manner via parameters and scaling of the two-electron two-center integrals. We then generalize and compare how various ab initio wavefunction theory (WFT), Kohn–Sham density functional theory (DFT), and DFT-based tight-binding (TB, e.g. DFTB) methods address electron correlation. Our conclusion at the end of this analysis is that it may be beneficial and more consistent to treat correlation energy in SEMO methods explicitly.

We note that it has been done e.g. in MNDOC, but one of the issues with this method is that it is significantly slower than MNDO. Alternative approach would be to use machine learning for predicting correlation energy as in our Δ-learning method.

In this perspective, we suggest very different approach in analogy to DFTB. We propose to absorb the correlation energy in pair-wise explicit terms V_rep also containing the core–core repulsion energy and other contributions. In the resulting novel TB-SEMO methods total energy is calculated as the sum of orbital energies (the band energy) plus V_rep terms. This allows simplifying parametrization as it can now separately target various types of properties. At the first stage, the SEMO part of a TB-SEMO method is optimized only on ionization potentials and dipole moments (or other one-electron properties). At the second-stage, the pair-wise potentials V_rep are parametrized to reproduce atomization energies, heats of formation, and geometries.

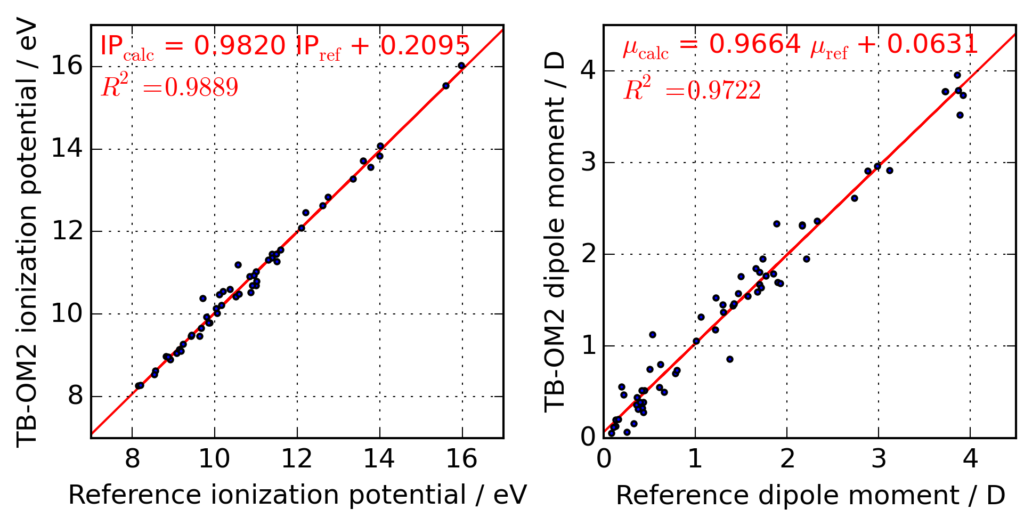
In our article, we designed proof-of-principle TB-SEMO method based on OM2, which is one of the most robust NDDO-based methods. The resulting prototype method (TB-OM2) has remarkable accuracy for one-electron properties it was trained on and the pair-wise potentials V_rep showed correct short-range character.

1. Johannes T. Margraf, Pavlo O. Dral, What Is Semiempirical Molecular Orbital Theory Approximating? J. Mol. Model. 2019, 25, 119. DOI: 10.1007/s00894-019-4005-8.